Bạn được cho một mảng gồm n guyên dương. Việc của bạn là tìm hai số nguyên sao cho ước chung lớn nhất của chúng càng lớn càng tốt.
Input:
- Dòng đầu tiên là một số nguyên n: kích thước của mảng.
- Dòng thứ hai chứa n số nguyên x1, x2, ..., xn: các phần tử của mảng.
Output: In ra ước chung lớn nhất tối đa.
Constraints:
- 2 <= n <= 2 * 10~^5~.
- 1 <= xi <= 10~^6~.
Ví dụ:
Input Output
5 7
3 14 15 7 9
Cho số nguyên dương N (N <= 2 * 10~^9~).
Yêu cầu: Đếm số lượng ước số của N và tổng các ước số của N.
Input: Số nguyên dương N
Output: Chứa hai số nguyên là số lượng ước số và tổng các ước của N.
Ví dụ:
Input Output
10 4 18
Giải thích: Số 10 có ước là 1 2 5 10 và tổng 1 + 2 + 5 + 10 = 18
Cho mảng ~A~ gồm ~n~ phần tử phân biệt. Gọi ~B~ là mảng ~A~ sau khi sắp xếp không giảm.
Gọi ~C_i~ là vị trí trên mảng ~A~ sao cho ~B_i = A_{C_i}~.
Hãy tính mảng C, hay nói cách khác là hãy cho biết vị trí ban đầu trên mảng A của mỗi phần tử trên B.
Input:
- Dòng đầu tiên in ra số n (n <= 100000).
- Dòng thứ hai in ra n số nguyên A1, A2, ..., An (1 <= Ai <= 10^9).
Output: In ra một dòng duy nhất gồm n số nguyên C1, C2, ..., Cn.
Scoring:
- Subtask 1 (30% số điểm): n <= 1000
- Subtask 2 (30% số điểm): Ai <= 1000000
- Subtask 3 (40% số điểm): không có giới hạn nào khác
Ví dụ:
Input Output
3 3 1 2
2 3 1
Vào một buổi sáng, rất tình cờ Nam nhìn thấy một số nguyên dương N trên đường từ nhà đến trường. Vì Nam rất thích số 30 nên Nam muốn biến đổi số N thành số M có dạng là số lớn nhất và là bội của số 30 bằng cách thay đổi vị trí của các chữ số trong số N mà Nam nhìn thấy.
Bạn hãy hỗ trợ Nam bằng cách viết chương trình để tìm số M (nếu nó tồn tài).
Input: Gồm một dòng duy nhất chứa số nguyên N (N có tối đa là 10^5 chữ số).
Output: In ra số M tìm được. Nếu không tồn tại M thì in ra -1
Ví dụ:
Input Output
30 30
----------
102 210
----------
3333333333333333333333333333 -1
Cho một dãy gồm N số nguyên dương  và số K (K <= N). Hãy in ra số nhỏ thứ K trong dãy.
và số K (K <= N). Hãy in ra số nhỏ thứ K trong dãy.
Input:
- Dòng đầu chứ số N, K.
- Dòng thứ hai chứa N số nguyên dương A1, A2, ..., An.
Output: Một dòng chứa dãy số nhỏ thứ K trong dãy.
Ví dụ:
Input Output
6 4 91
91 451 43 3 452 54
Nhập xâu họ tên s, hãy chuẩn hóa lại xâu họ tên đó. Xâu họ tên là xâu chuẩn hóa khi thỏa mãn các điều sau:
- Không có dấu cách thừa
- Chữ cái đầu mỗi từ viết in hoa còn lại là in thường.
Input: Xâu họ tên s
Output: Xâu sau khi chuẩn hóa
Ví dụ:
Input Output
nGuyEN thANH tUNG Nguyen Thanh Tung
Tên file: NAME.***
Nhập xâu s. Thống kê số các chữ số '0', số chữ số '1', …, số chữ số '9' trong xâu đó.
Input: Một xâu s
Output: Một dòng gồm 10 số nguyên, trong đó số thứ i là k thể hiện số i - 1 xuất hiện hiện k lần trong xâu.
Ví dụ:
Input Output
ab8 jf0kl0 fsf1 fsff9 lort 5 klwr9 klkf6 2 1 0 0 0 1 1 0 1 2
Tên file: BCOUNT.***
An xây dựng cho mình một phép nhân như sau: A * B thay vì thực hiện một phép nhân thông thường thì cậu ta lại lấy các chữ số của A nhân với các chữ số của B rồi sau đó cộng các tích đó lại với nhau.
Ví dụ: kết quả của phép nhân 123 x 45 là: 1 x 4 + 1 x 5 + 2 x 4 + 2 x 5 + 3 x 4 + 3 x 5 = 54
Yêu cầu: cho hai số nguyên dương A và B. Hãy cho biết giá trị của A*B theo phép nhân của bạn An.
Input: Hai số nguyên dương A và B (1 ≤ A, B ≤ 10^9)
Output: Ghi ra kết quả tìm được:
Ví dụ:
Input Output
123 45 54
Tên file: mult.***
Cho số nguyên dương N. Gọi K là tổng các chữ số của N. Hãy kiểm tra xem K có phải là số nguyên tố không?
Input: Nhập N
Output: Đưa ra thông báo: "YES" nếu k là số nguyên tố, "NO" trong trường hợp ngược lại
Ví dụ:
Input Output
16 YES
----------
9 NO
Giải thích:
- 16 có tổng các chữ số là 7. Khi đó 7 là số nguyên tố
- 9 có tổng các chữ số là 9. Khi đó 9 không là số nguyên tố.
Tên file: ngto2.***
Nhập hai số nguyên dương a và b. Sau đó hiện phân số tối giản của phân số a / b .
Input: Một dòng chứa hai số nguyên dương a và b
Ouput: Hiện ra phân số tối giản
Ví dụ:
Input Output
10 25 2/5
Tên file: pstoigian.***
Cho dãy số gồm N phần tử nguyên A1, A2, ..., AN (1 <= n <= 10^3). Hãy đếm cặp số (có thể không liên tiếp) có tổng bằng là một số nguyên tố.
Input:
- Dòng đầu tiên nhập số N
- Dòng tiếp theo nhập các số A1, A2, …, AN
Output:
- Một số duy nhất là số lượng cặp số liên tiếp có tổng là một số nguyên tố
Ví dụ:
Input Output
5 3
9 6 -2 9 1
Tên file: capso3.***
Nhập vào dãy số thực. In ra dãy đã được sắp xếp tăng dần, giảm dần.
Input:
- Dòng 1 chứa giá trị n (1 <= n <= 1000)
- Dòng 2 chứa n số thực a1, a2, ..., an
Output:
- Dòng 1 là dãy a sau khi được sắp xếp tăng dần
- Dòng 2 là dãy a sau khi được sắp xếp giảm dần
Ví dụ:
Input Output
4 1.00 2.00 3.00 4.00
3.00 2.00 4.00 1.00 4.00 3.00 2.00 1.00
Tên file: ARRSORT.***
Nhập một số nguyên dương N. Đếm và hiện ra màn hình các số nhỏ hơn hoặc bằng N là số chẵn và chia hết cho 3.
INPUT: Số N (1 <= N <= 1000)
OUTPUT:
- Dòng 1 hiện số lượng số chẵn chia hết cho 3 <= N
- Dòng 2 hiện các số chẵn chia hết cho 3 <= N.
Ví dụ:
Input Output
15 2
6 12
Tên file: SOCHAN.***
Anh Bo có một số tiền là n đồng. Anh định đem n đồng này gửi ngân hàng với lãi suất 10% một năm. Cứ sau mỗi năm anh sẽ ra ngân hàng rút tiền lãi rồi nhập chung với tiền gốc để gửi lại cho năm sau. Anh dự định khi nào đủ số tiền m đồng thì sẽ rút toàn bộ để đi mua bò. Hỏi sau mấy năm thì anh Bo sẽ có đủ tiền mua bò?
Dữ liệu nhập: Là hai số nguyên n và m (10 ≤ n ≤ m ≤ 10~^9~)
Dữ liệu xuất: Là số năm cần gửi ngân hàng.
Ví dụ:
Input Output
100 160 5
Giải thích ví dụ:
Sau năm 1: 110 đồng
Sau năm 2: 121 đồng
Sau năm 3: 133 đồng
Sau năm 4: 146 đồng
Sau năm 5: 161 đồng
Tên file: NGANHANG.***
Cho hai số nguyên N và M. Tìm UCLN của N và M.
Input: Hai số M và N ( |M| <= 10~^9~, |N| <= 10~^9~)
Output: UCLN của M và N
Ví dụ:
Input Output
2 2000000000 2
-36 -81 9
Tên file: UCLN.***
Bàn cờ vua là một hình vuông gồm n x n ô. Để dễ dàng cho các đấu thủ trong việc chơi cờ. Người ta tô màu ô đen xen kẽ với ô trắng.

Yêu cầu: Cho số nguyên n, hãy vẽ bàn cờ vua kích thước n x n. Biết rằng ô đầu tiên ở góc trên bên trái là ô trắng.
Dữ liệu nhập:
- Là số nguyên n ( 1 ≤ n ≤ 100)
Dữ liệu xuất:
- Gồm n dòng, mỗi dòng gồm n ký tự B (màu đen) hay W (màu trắng)
Ví dụ:
Input Output
4 WBWB
BWBW
WBWB
BWBW
5 WBWBW
BWBWB
WBWBW
BWBWB
WBWBW
Tên file: COVUA.***
Năm 2112, nước ta đã trở thành một cường quốc kinh tế nhưng giá điện lại vô cùng đắt đỏ. Công ty NVE là nhà cung cấp điện duy nhất trong thành phố nơi Nam ở. NVE vừa tăng giá điện, bảng giá như sau:

Cách tính : 100kWh đầu tiên có giá 2000VNĐ mỗi kWh, 100 kWh tiếp theo (từ 101-200) có giá 3000 VNĐ mỗi kWh. Cứ như vậy tính tiếp.
Ví dụ: nếu sử dụng 250 kWh thì bố mẹ của Nam phải trả:
2000 x 100 + 3000 x 100 + 5000 x 50 = 750000 (VNĐ).
Tháng này, gia đình Nam dùng hết x số điện. Vậy gia đình Nam phải trả cho công ty điện lực số tiền là bao nhiêu?
INPUT:
- Một số nguyên dương duy nhất x (x ≤ 100000) là số kWh điện mà gia đình của Nam đã sử dụng.
OUTPUT:
- Một số nguyên duy nhất là số tiền mà bố mẹ của Nam phải trả cho công ty NVE.
Ví dụ:
Input Output
250 750000
Tên file: BILL. ***
Hai bạn Bắc và Nam chơi trò chơi oản tù tì, trong quá trình chơi mỗi người chơi sẽ đưa ra một trong ba hình dạng của bàn tay là: búa, kéo và bao. Trong đó luật chơi được mô tả như sau:
- Người chơi ra hình búa sẽ thắng người chơi ra hình kéo.
- Người chơi ra hình kéo sẽ thắng người chơi ra hình bao.
- Người chơi ra hình bao sẽ thắng người chơi ra hình búa.

Hai người chơi ra hình giống nhau thì sẽ hòa. Tại một lượt chơi, hai bạn Bắc và Nam sẽ đưa ra một hình dạng bàn tay của mình. Em hãy lập trình cho biết kết quả ai là người thắng, hoặc hai bạn hòa nhau.
INPUT: Gồm hai số nguyên a và b (0 ≤ a, b ≤ 2). Trong đó 0 nếu đó là búa, 1 nếu đó là kéo, 2 nếu đó là bao Số a là ký hiệu hình bàn tay của bạn Bắc, số b là ký hiệu hình bàn tay của bạn Nam
OUTPUT:
- Nếu bạn Bắc thắng thì đưa ra từ "BAC".
- Nếu bạn Nam thắng thì đưa ra từ "NAM".
- Nếu hai bạn hòa nhau thì đưa ra từ "HOA".
- Chú ý kết quả đưa ra là chữ in hoa.
Ví dụ:
Input Output
0 0 HOA
0 1 BAC
1 0 NAM
Tên file: GAMES.***
Một khu đất hình chữ nhật có cạnh là a và b. Người ta xây một khu vui chơi hình tròn tại vị trí trong khu đất như hình vẽ.
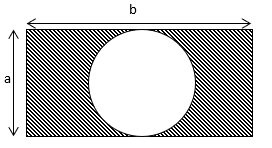
Hỏi rằng khu đất còn lại (phần gách chéo) có diện tích bằng bao nhiêu. Biết rằng giá trị pi = 3.14
INPUT:
- Hai số thực a, b được viết trên cùng 1 dòng
OUTPUT:
- Diện tích phần gạch chéo tính được, kết quả lấy 2 chữ số ở phần thập phân.
Ví dụ:
Input Output
2.00 4.00 4.86
Tên file: AREA0.***
Theo quy định của nhà trường, mỗi trường hợp không đeo thẻ học sinh sẽ bị trừ a điểm thi đua của lớp, mỗi trường hợp nói chuyện trong lớp bị trừ b điểm thi đua và mỗi trường hợp đi học muộn bị trừ c điểm. Sổ đầu bài ghi nhận trong tháng có t trường hợp không đeo thẻ, n trường hợp nói chuyện riêng, và m trường hợp đi học muộn.
Hãy nhập các giá trị a, b, c, t, n, m từ bàn phím và tính tổng điểm bị trừ thi đua trong tháng đó.
Input:
- Các giá trị a, b, c, t, n, m
Output:
- Kết quả bị trừ thi đua trong tháng
Ví dụ:
Input Output
1 1 1 1 1 1 3
Tên file: NOIQUY.***